Построение точки пересечения прямой и плоскости
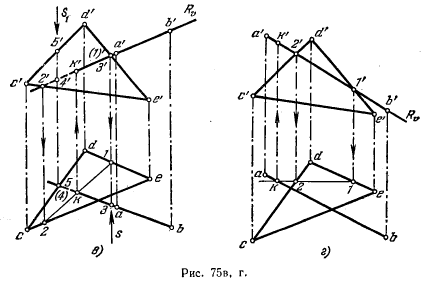
Линия пересечения двух плоскостей — прямая линия. Рассмотрим сначала частный случай рис. Если одна из плоскостей параллельна фронтальной плоскости проекций рис.



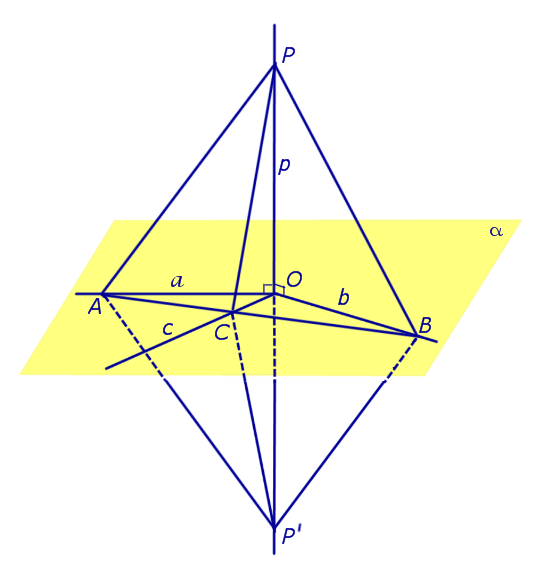
Плоскость общего положения — это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций. Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций. Плоскость частного положения — плоскость, перпендикулярная или параллельная плоскости проекций. Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии. Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости Рисунок 3.
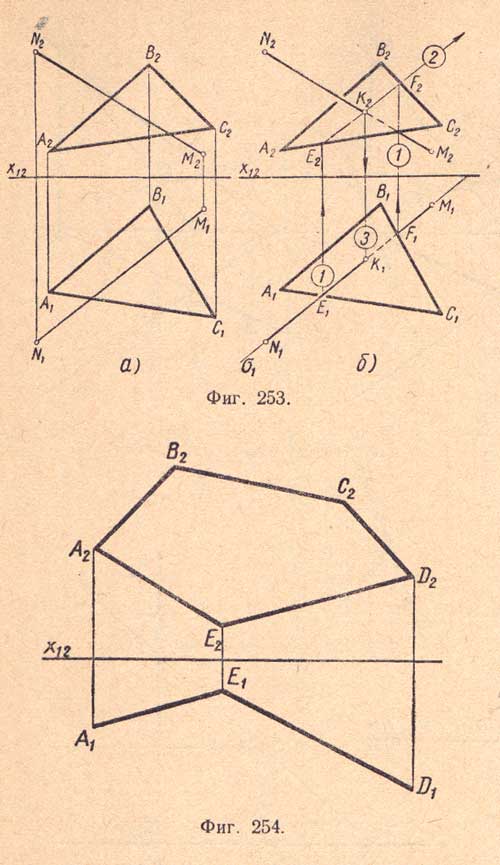
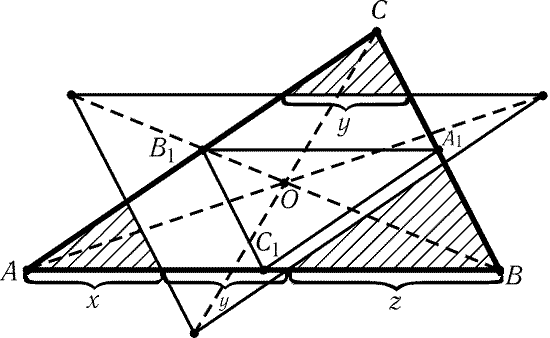
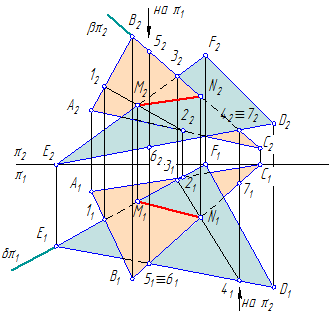
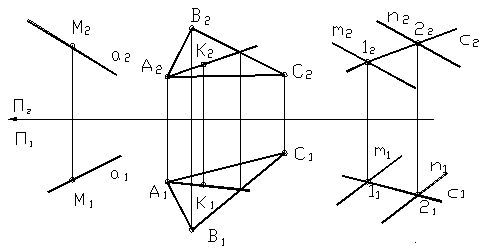
- Построение линии пересечения двух треугольников.
- Точка пересечения стороны В-С на фронтальной плоскости проекций не определяется ввиду ее профильного положения. Заменив в плоскости треугольника сторону В-С на прямую общего положения С-5 , определяем вторую точку 6 линии пересечения плоскостей 2.
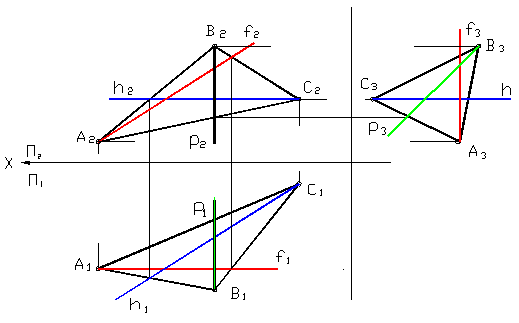
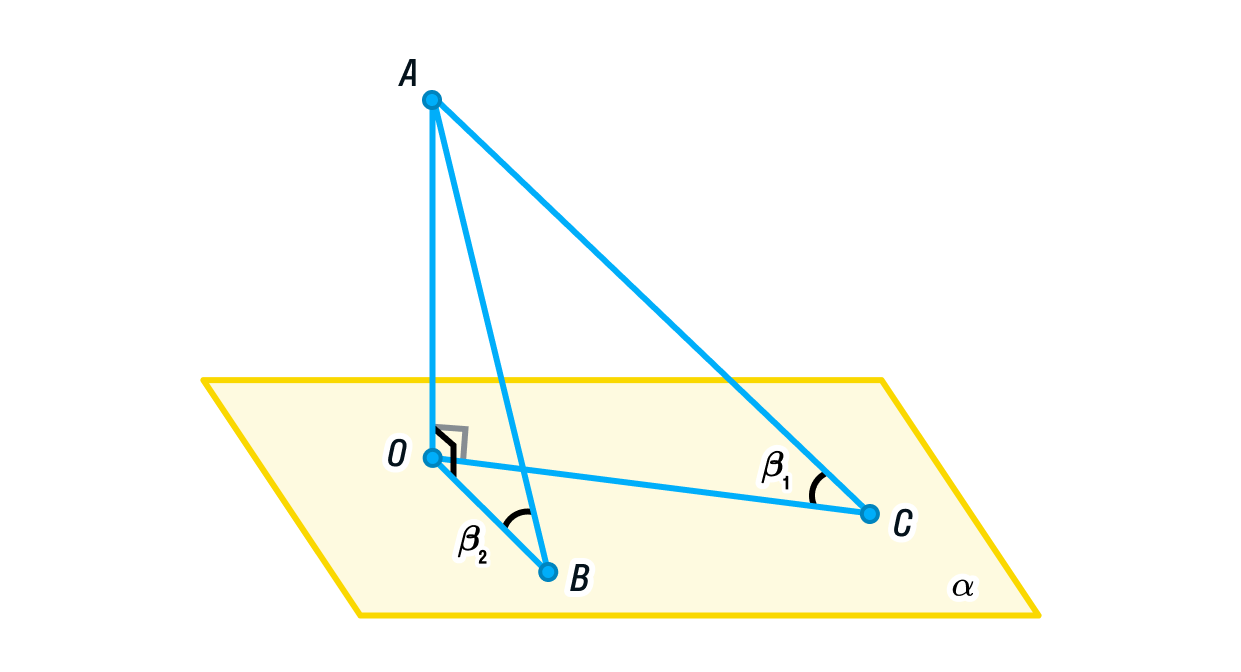
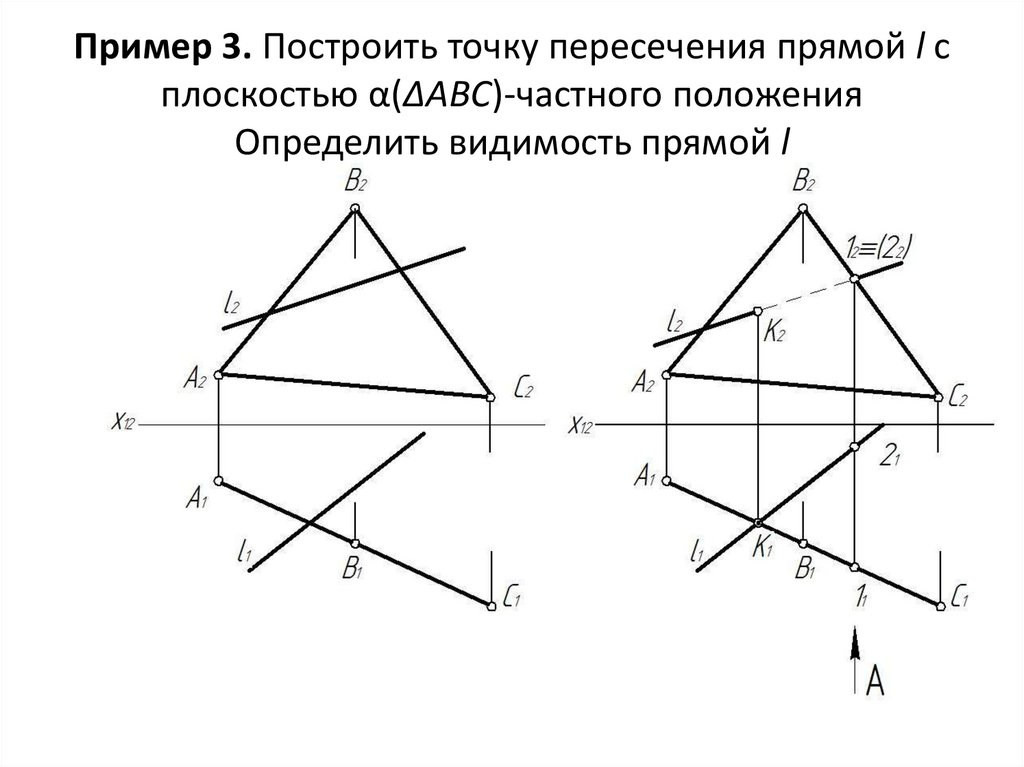
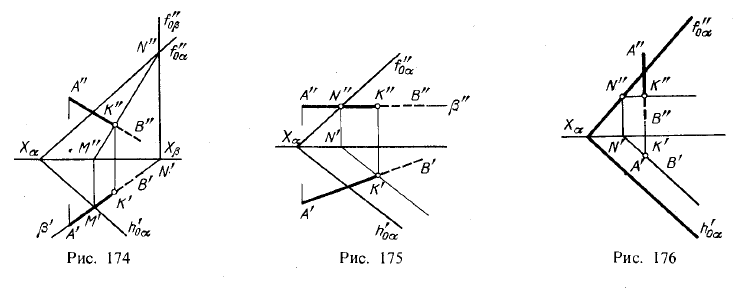
- Как известно, для нахождения точки пересечения прямой с плоскостью общего положения следует через прямую провести вспомогательную плоскость R , построить линию пересечения этой плоскости с заданной 1—2 и найти. Точка К является искомой точкой пересечения прямой с плоскостью рис.
- Измерительные инструменты и обмер деталей. Щупы для определения величины зазора.
- 3.2. Плоскости частного положения
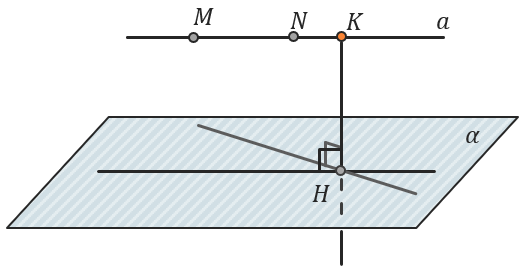
- Прямая линия в пространстве может принадлежать плоскости этот случай был рассмотрен ранее в пункте 3.
- Рассмотрим пошаговую инструкцию построения точки пересечения прямой общего положения с плоскостью общего положения. Отметим, что построение точки пересечения прямой и плоскости - это одна из основ решения задач по предмету начертательная геометрия , не освоив которую дальнейшее понимание предмета будет достаточно трудным.
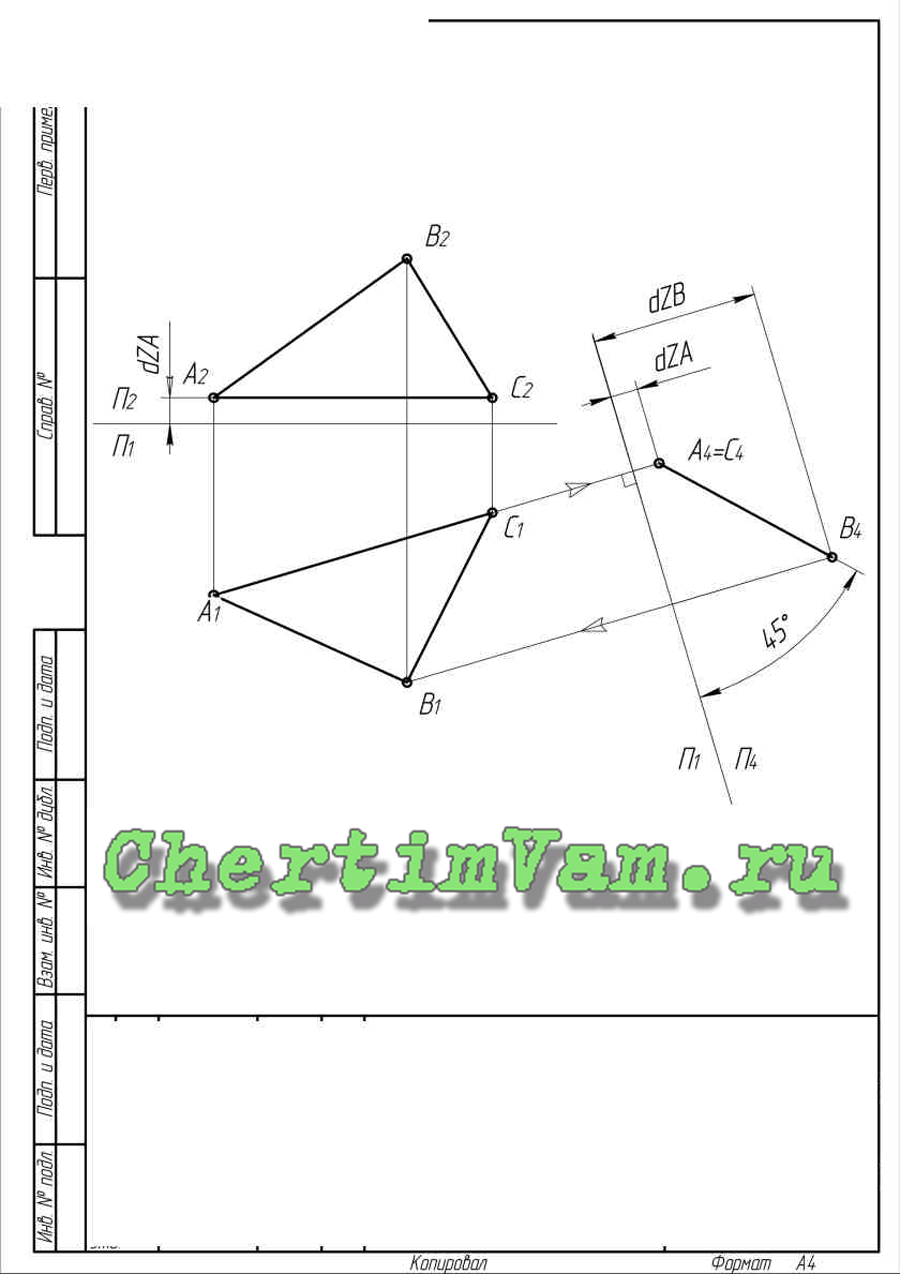
- Строим проекции треугольника АВС. Строим проекции треугольника EDK.
- 3.8 Параллельность прямой и плоскости
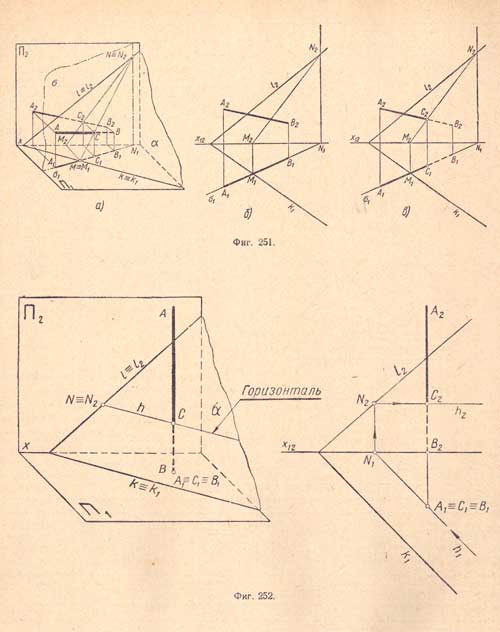
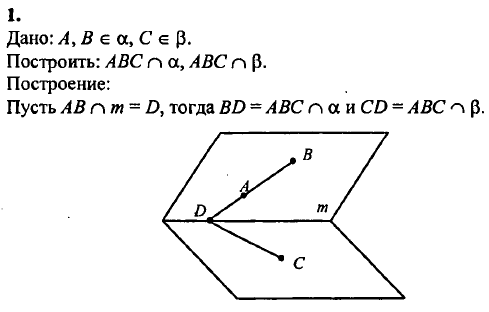
- Две плоскости пересекаются друг с другом по прямой линии. Чтобы её построить, необходимо определить две точки, принадлежащие одновременно каждой из заданных плоскостей.
- Аналитическая геометрия для «чайников».
- Прямая может принадлежать плоскости см.
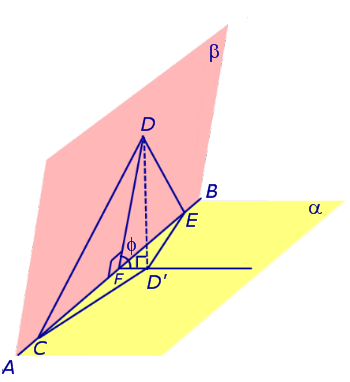



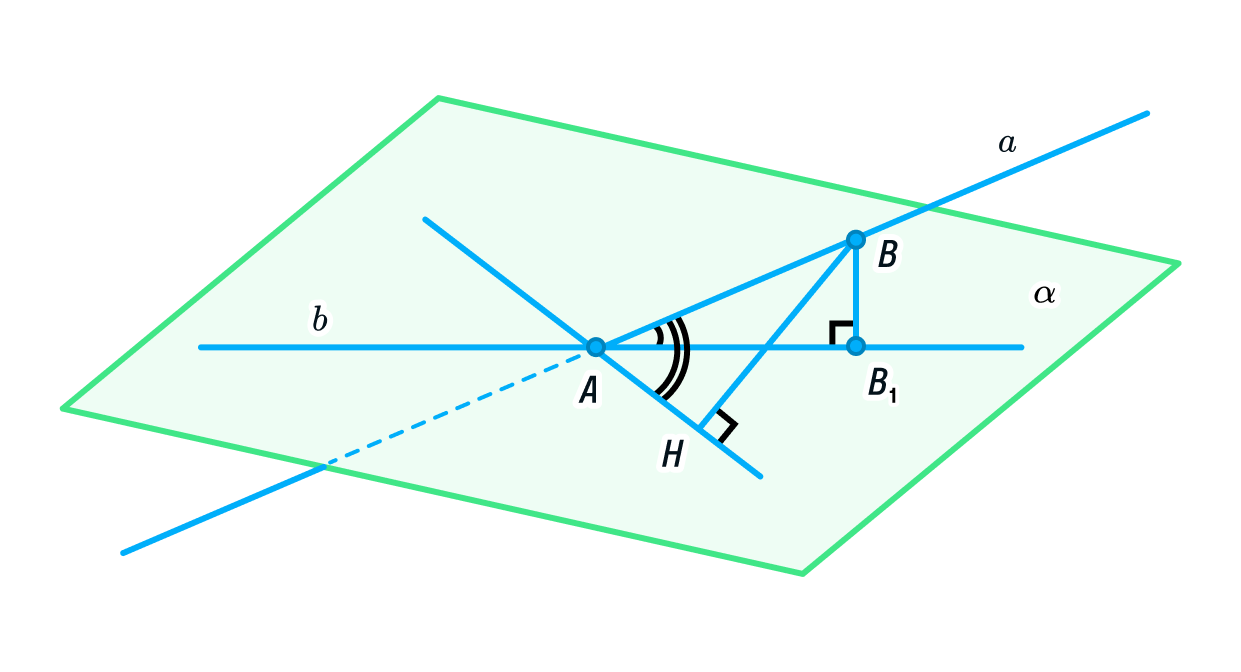
Прямая линия в пространстве может принадлежать плоскости этот случай был рассмотрен ранее в пункте 3. При пересечении прямой линии с плоскостью следует выделить частный случай, когда прямая перпендикулярна плоскости. Первый случай был разобран в пункте 3.