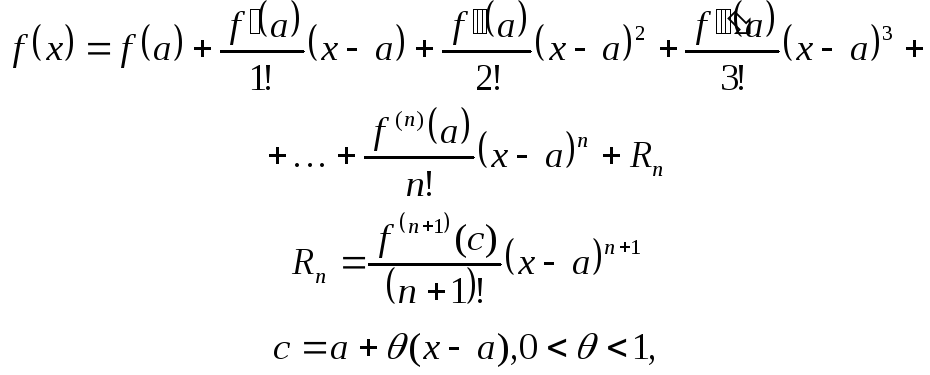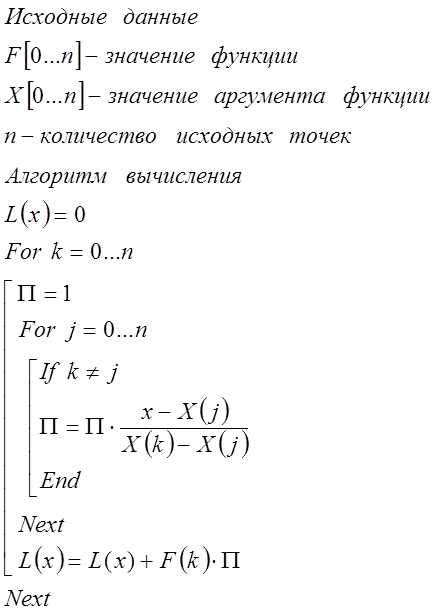Формула Тейлора. Остаточный член в виде Лагранжа. Разложение элементарных функций
Ост а точный чл е н приближённой формулы, разность между точным и приближённым значениями представляемого этой формулой выражения. В зависимости от характера приближённой формулы О. Обычно задача исследования О. Например, приближённой формуле.







Новые калькуляторы Построить график функции Точки разрыва функции Построение графика методом дифференциального исчисления Упростить выражение. Примеры решений Интервал сходимости ряда Оригинал и его изображение Найти предел Точки разрыва функции Диф уравнения онлайн Разложение в ряд Фурье Разложение в ряд Тейлора Найти производную. Математика онлайн Математика онлайн Линейная алгебра Вычислительная математика Теория вероятностей Математическая статистика Статистика онлайн. Действия Загрузить предыдущие.




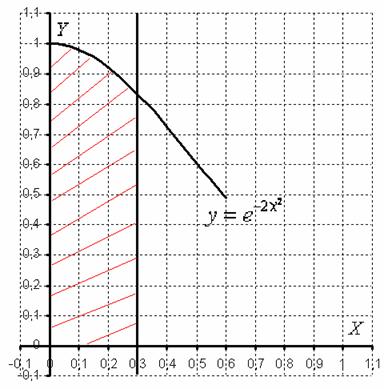






Частный случай разложения в ряд Тейлора в нулевой точке называется рядом Маклорена. Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка. Обобщением понятия ряда Тейлора в функциональном анализе является ряд Фантапье. Функция называется аналитической на промежутке на множестве , если она является аналитической в каждой точке этого промежутка множества.