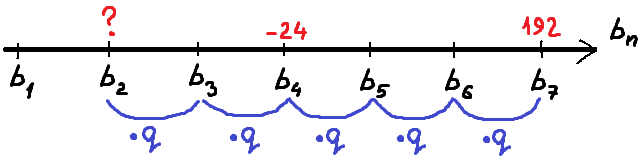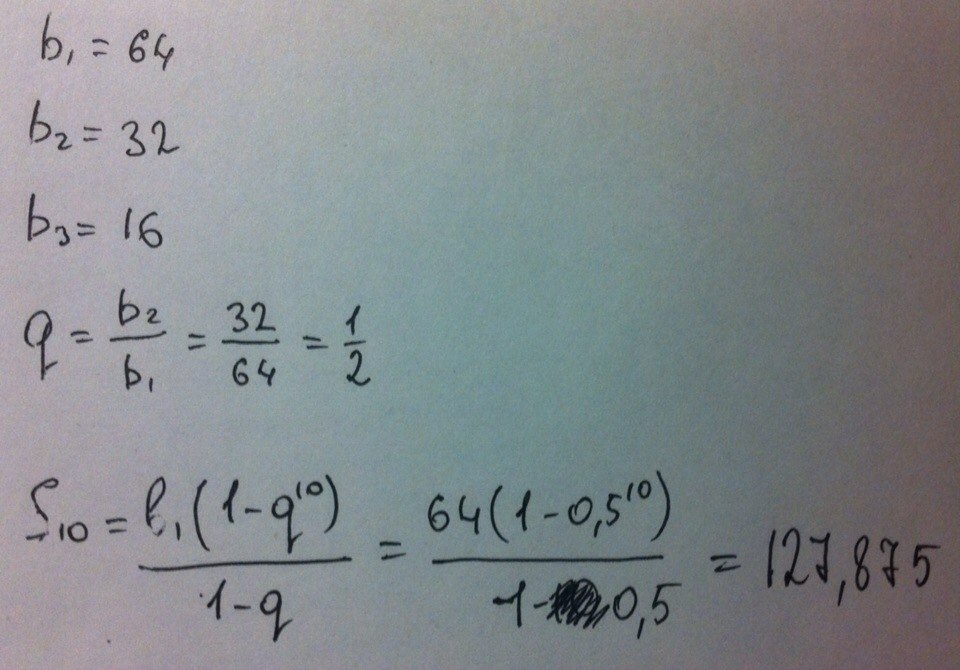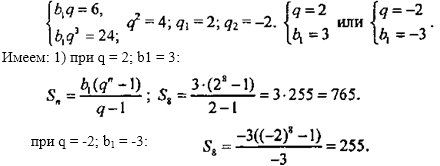
Арифметическая и геометрическая прогрессия. 9 класс. Часть 2 (Методическое пособие)
Алгебра 9 кл. БП Найти. По тексту вопроса. По дисциплине. Найдите значение х, при котором числа х —1, , 6х образуют конечную геометрическую прогрессию.
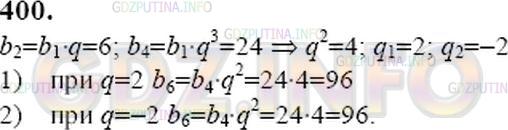


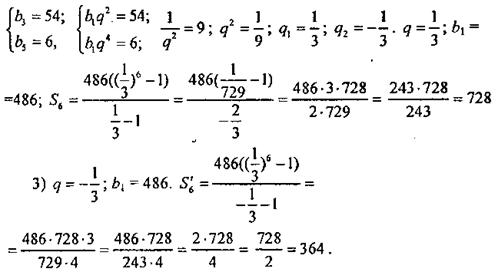






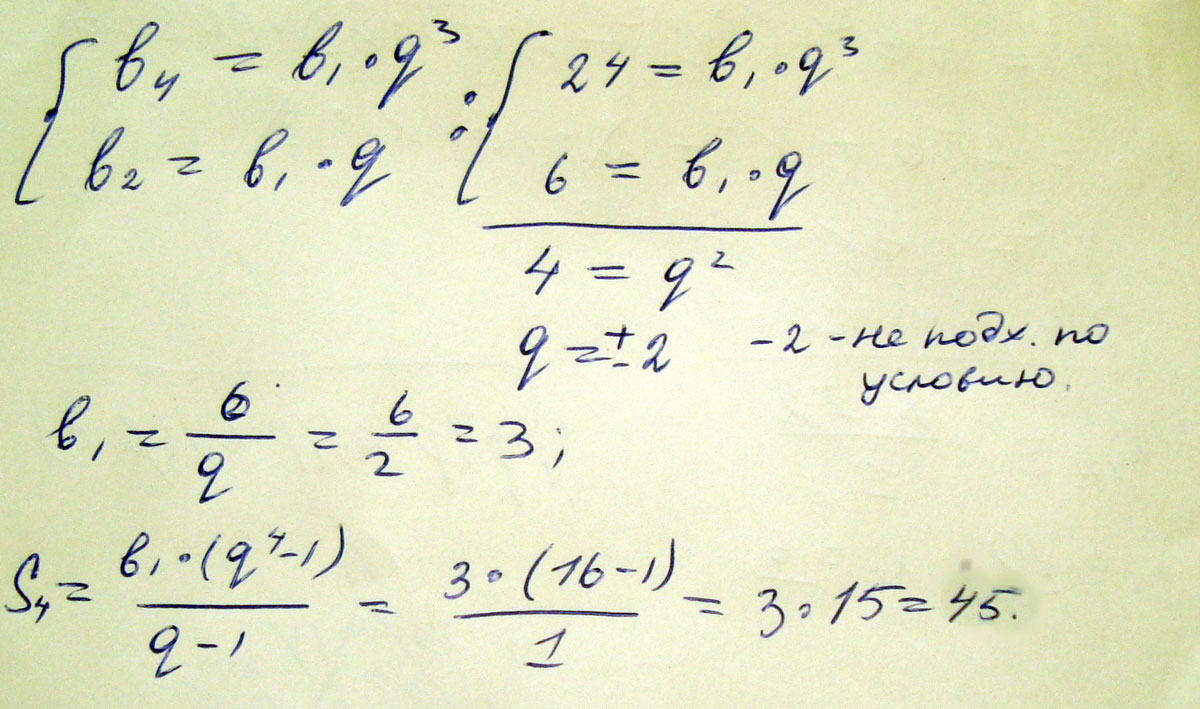


Оформить бесплатно документ можно здесь. Если каждому натуральному числу n отнесено по некоторому закону число x , то говорят, что задана числовая последовательность : ,, , …,. Числа , называются членами последовательности, они не обязательно различны между собой. Зная её, мы можем получить любой член последовательности. Для этого достаточно в правую часть формулы вместо n подставить номер искомого члена. Какое из следующих чисел является членом этой последовательности?







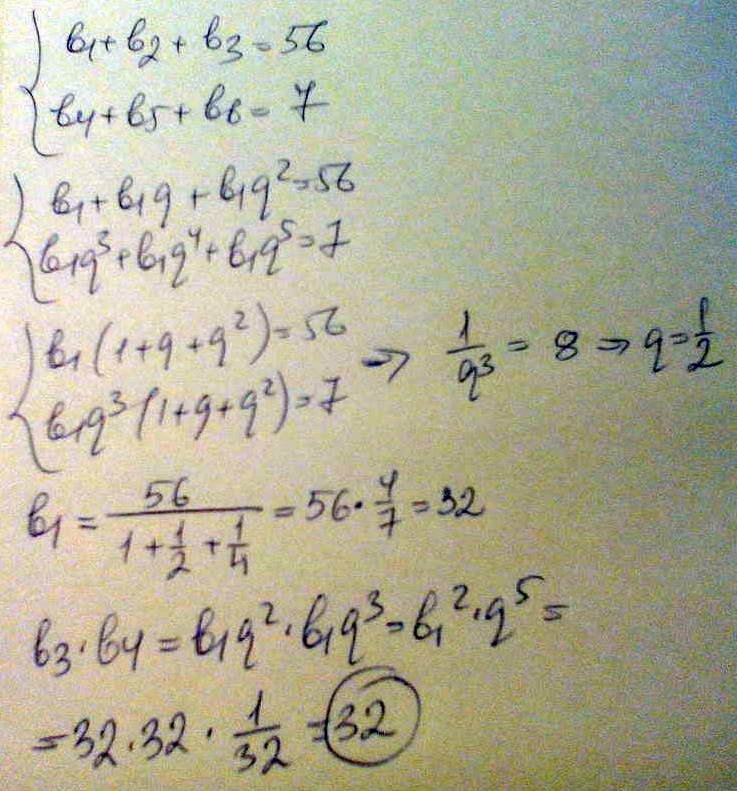





Тогда складывайте последовательно все члены пока не получится Следовательно сумма первых 6 равна данному значению. Главная История математики. Арифметическая прогрессия Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же для данной последовательности числом, называется арифметической прогрессией. Примером арифметической прогрессии является натуральный ряд чисел 1, 2, 3, Каждое его число, начиная со второго, равно предыдущему, сложенному с единицей.