Уравнение медианы треугольника
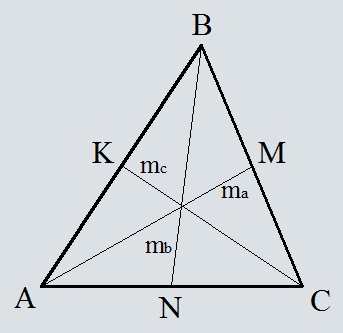
Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Так как каждая вершина треугольника имеет свою медиану, то всего в треугольнике может быть три медианы. Длину медианы треугольника ABC если известны все стороны треугольника можно расчитать по одной из нижепреведённых формуле:. Так же данные формулы можно встретить в такой записи, что по сути является тем же самым что формулы выше:. Медиана треугольника Калькулятор для вычисления медианы треугольника. Из какой вершины треугольника опустить медиану:.




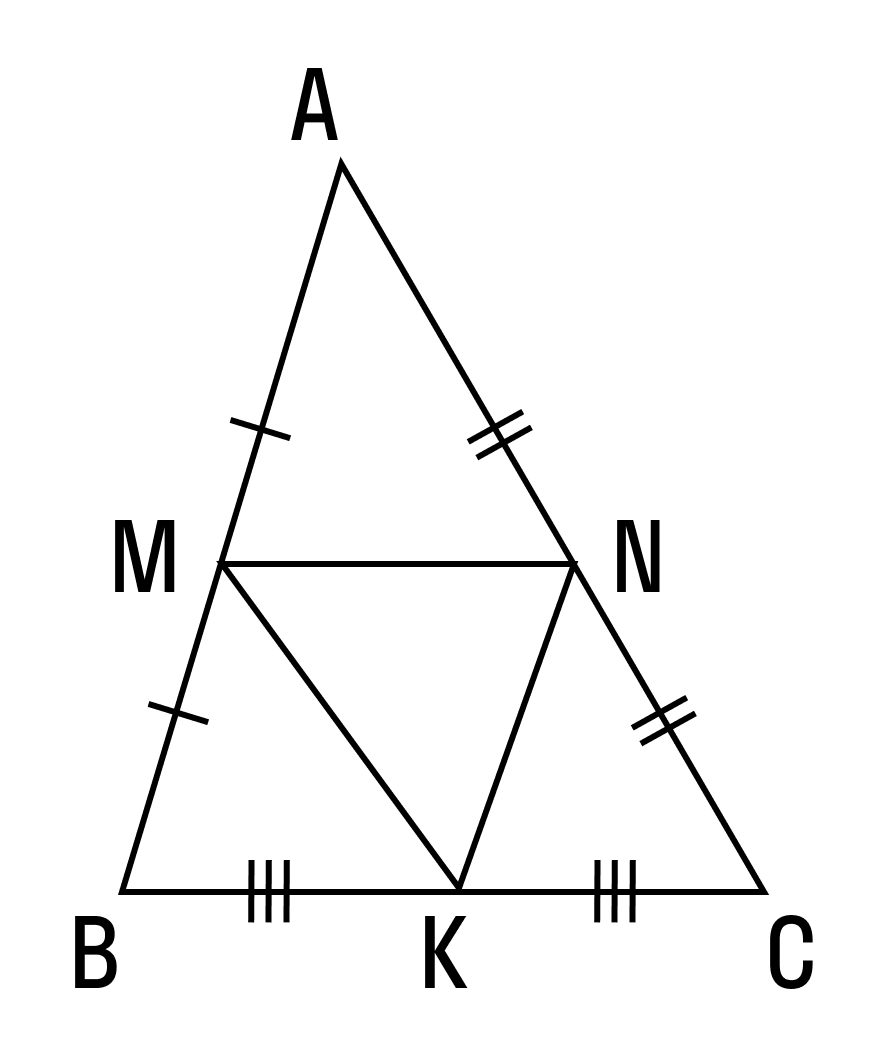
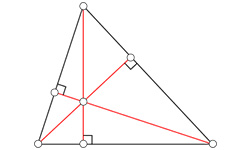
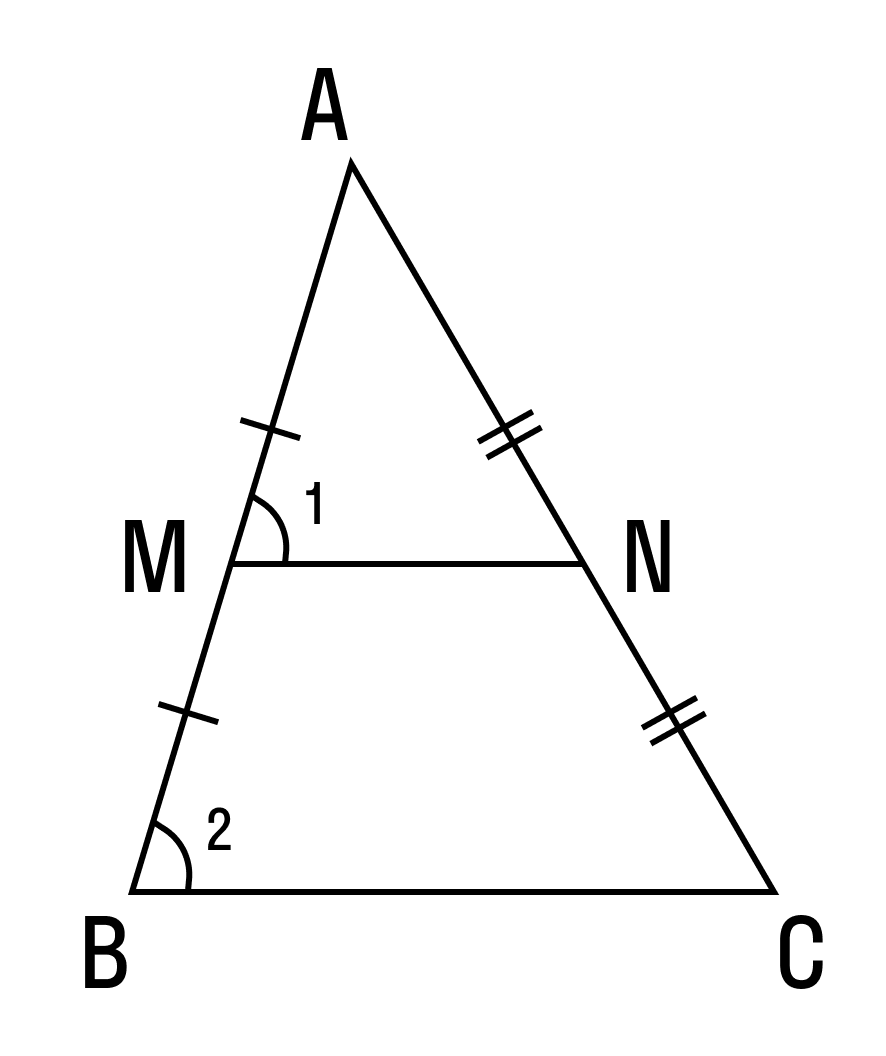

Медиана являет собой внутренний линейный сегмент треугольника, геометрически выраженный через отрезок, соединяющий в геометрической фигуре вершину и срединную точку противоположной стороны. Не следует путать медиану в геометрии с медианой в статистике — это совершенно разные величины. Калькулятор дает возможность вычислить медиану по заданным при заполнении полей его формы координатам вершин треугольника. Особенностью точки пересечения медиан в треугольнике является ее принадлежность к центру масс центру тяжести данной геометрической фигуры.
- Медиана треугольника - это отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. У каждого треугольника есть ровно три медианы, для каждой вершины, и все они пересекаются в центре треугольника.
- Медиана соединяет вершину треугольника с серединой противолежащей стороны.
- Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
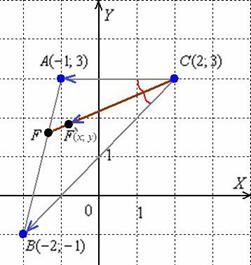
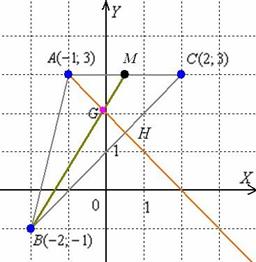
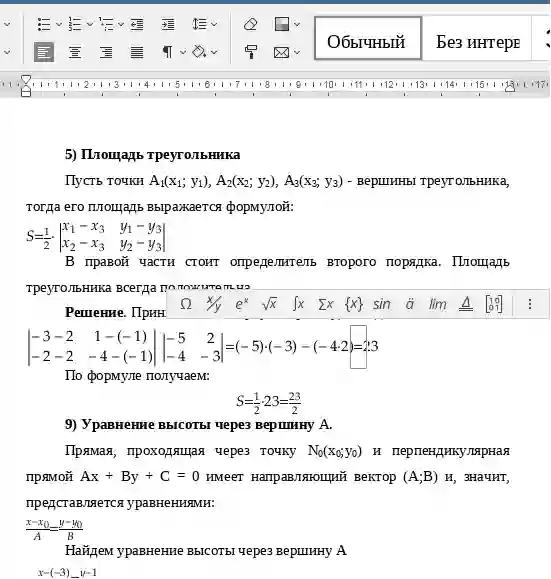
- Даны координаты вершин треугольника АВС. Найти длины медианы, высоты, биссектрисы, проведенные из вершин А Даны координаты вершин треугольника АВС.
- Медиана — отрезок, опущенный из вершины треугольника на середину противоположной стороны. В треугольнике можно провести 3 разные медианы, которые пересекутся в одной точке, делящей каждую медиану в пропорции , считая от вершины.
- Новые калькуляторы Вращение пирамиды Построить график функции Точки разрыва функции Упростить выражение.
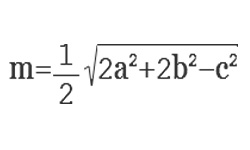




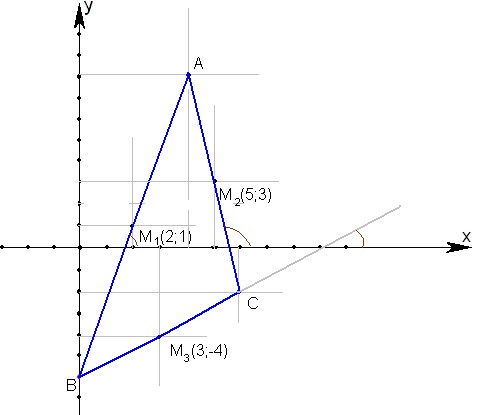


| 407 | Медиана треугольника выходит из угла и делит противолежащую сторону пополам. | |
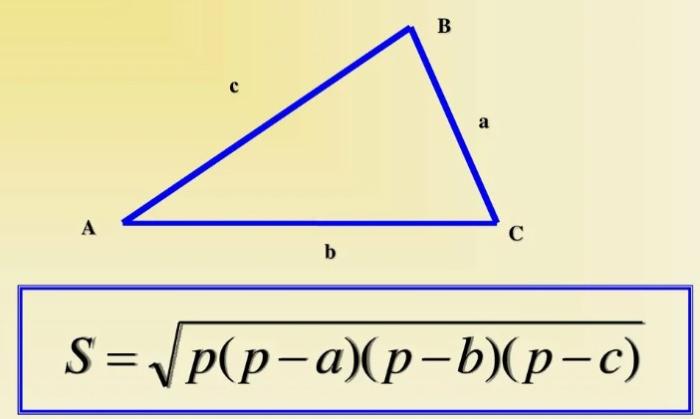
| 78 | Этот онлайн калькулятор позволит вам очень просто найти площадь треугольника построенного на векторах. Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление площади треугольника построенного на векторах и закрепить пройденный материал. | |
| 74 | Медиана треугольника представляет собой отрезок, который соединяет любую вершину треугольника с серединой противоположной стороны. В каждом треугольнике есть три разные медианы, пересекающиеся в одной точке, которая лежит внутри треугольника. | |
| 176 | Медиана треугольника лат. Каждый треугольник имеет ровно три медианы , по одной из каждой вершины, и все они пересекаются друг с другом в центре треугольника. | |
| 171 | Список статей » Список форумов. Этот сервис может не работать в браузере Internet Explorer. | |
| 111 | Формула расчета медианы треугольника. Собственно, формула медианы:. | |
| 89 | В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника заданного вершинами или сторонами : уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т. Другие решения по аналитической геометрии на плоскости. | |
| 96 | ||
| 295 | ||
| 448 |